Finding the Least Common Multiple Visually, without Calculation

The alternative method described here is graphic. It requires no factoring or division. In fact, this visual method requires no computation whatsoever. Instead you apply the graphic method for finding the GCF, do some additional drawing, count and finally multiply two numbers.

This graphic method does not rely on knowing any common factors. It employs simple division and each division step is progressively simpler. Or, you may even use this method without ever using division. At most, if you so choose (as stated above), you only need subtraction.

This method has several advantages:

 
• Using graphics, this method provides a visual alternative for computational methods.

• It also provides a visual means to explain the concept of least common multiple (LCM) and why the various methods, including those that employ factoring, work.

• Being an alternative, it demonstrates that there are different ways to reach the same mathematical destination.

• This method demonstrates the close relationship between arithmatic and geometry.
 

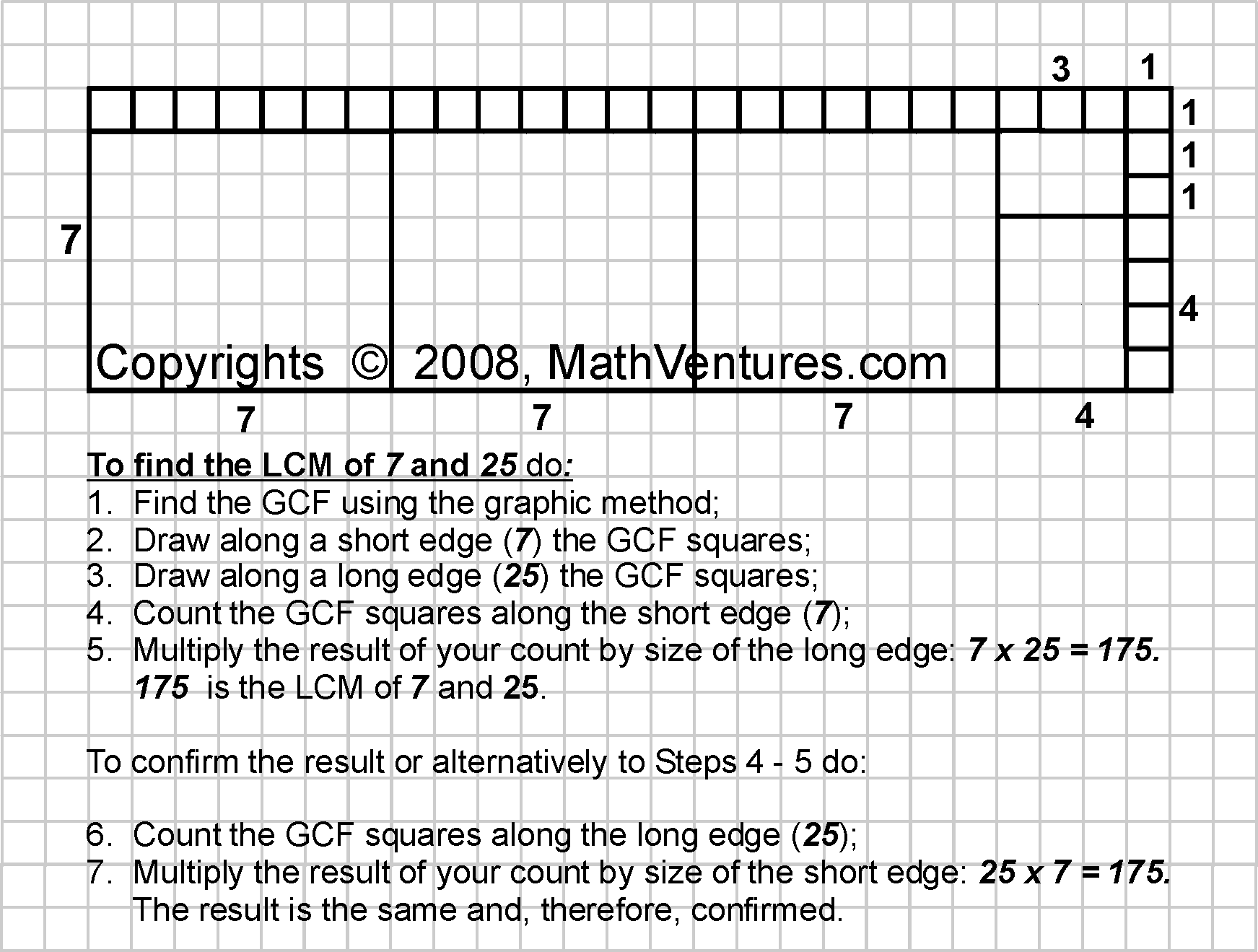
Since 7 and 25 have no common factor, and therefore they also do not have GCD,
we get their LCM by simply multiplying 7 by 25.
 
 

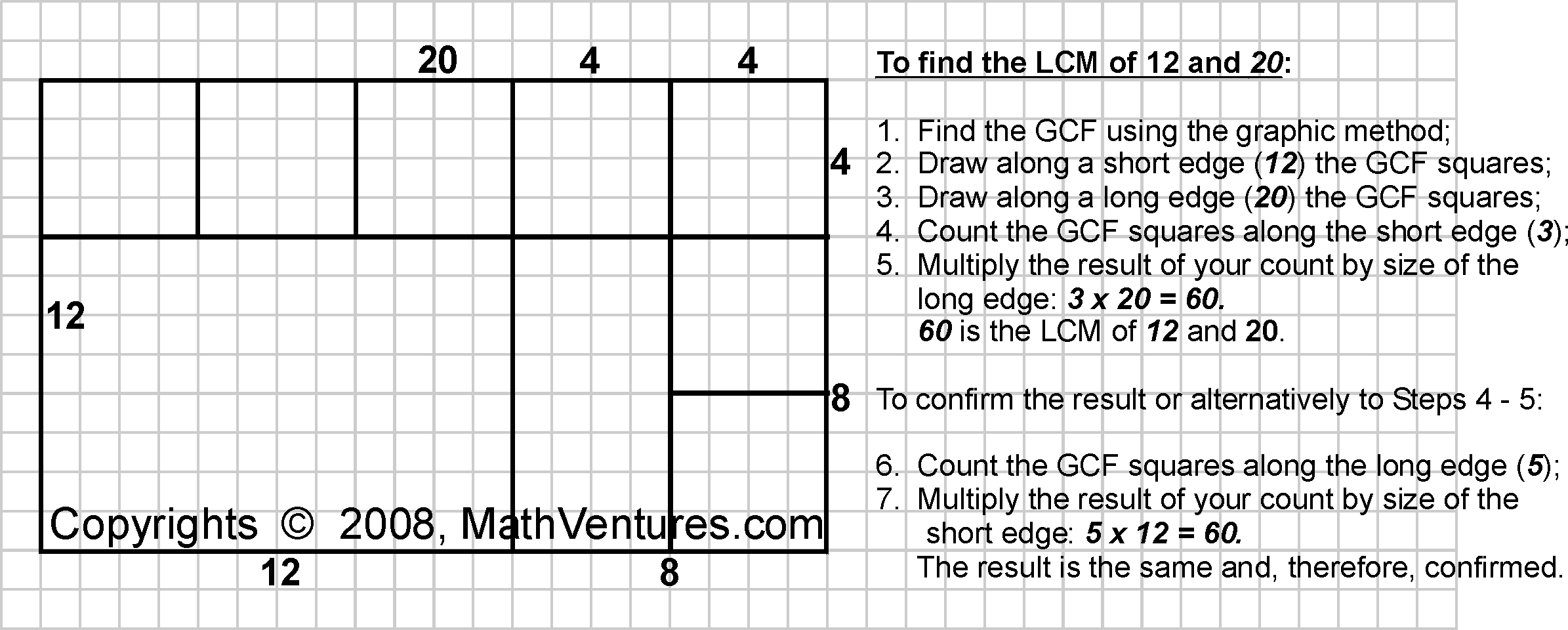
Look closely at the GCF (GCD) square, which you replicated along the edges of the original rectangle. What is the size of the GCF square, i.e. the length of one side of the GCF square? — As its name implies, the size of the GCF square is the greatest common factor of the two numbers that are represented by sides of the rectangle. In the first example the answer is 4 and in the second it is 1. This means that we can get the length of each side of the rectangle by multiplying the size the GCF square by the number of GCF squares along that edge, which we can call the GCF-square count. In the first case 4 x 5 = 20 and 4 x 3 = 12 in the second it is 1 x 7 = 7 and 1 x 25 = 25.

It is important to keep in mind that the size of each edge consists of the multiplication of the GCF by its GCF-square count. Therefore, when we multply the GCF-square count along one edge by the length of the other edge we exclude from the multiplication one occurance of the GCF (GCD). Examining the resulting product, we see that it always consists of the multiplication of these three numbers

• the GCF (GCD), by

• the GCF count along the short edge, by

• the GCF count along the long edge.

As we saw above, the product of the first and the second is the length of the short edge and the product of the first and the third is the length of the long edge.

This method provides a visual demonstration why the LCM equals the product of the two original numbers divided by their GCF (GCD).