The alternative method described here is graphic. It requires no division. In fact, as long as you draw to scale, this visual method requires no computation whatsoever.

This graphic method makes use of the relationship between geometry and arithmatic.

This method has several advantages:
 

• Using graphics, this method provides a visual alternative for computational methods.
• It also provides a visual means to explain the concept of greatest common factor/divisor (GCF/GCD) and why the various methods, including those that employ factoring, work.
• Being an alternative, it demonstrates that there are different ways to reach the same mathematical destination.
• This method demonstrates the close relationship between arithmatic and geometry.
• This method is simpler than those requiring factoring because no division is done.

When given two integers, m and n, the common methods to find their GCF (or GCD) is to divide both numbers by the most obvious factors (excluding 1) recursively until all are exhausted. Then GCF is equal to the product of all of the common factors. For example, say m and n are 36 and 60 respectively. Divide both numbers by 2. The results, 18 and 30, are also even so divide them by 2 again. This time you get 9 and 15, both of which are divisible by 3. If other obvious factors are known, such as 5, 9, 7 or 11, then divide by these factors. The problem is that often no factor is easily apparent for both m and n, especially when at least one of the numbers is larger than 12x12, which is the top of "math facts" with which students are required to fluent.This method is visual -- with it you find the greatest common factor without doing any calculation — you only need to know and to do is to draw to scale. Using graph paper or other means for greating a grid (e.g., snap cubes) you can still use this method; in this case all you need to know and do is count. You draw and the solution appears. When teaching visually-oriented students, who are experiencing difficulties understanding the computational method, employing this graphic method, is often easier.

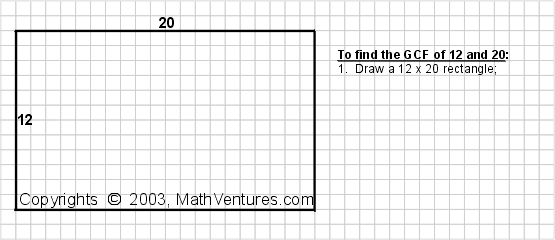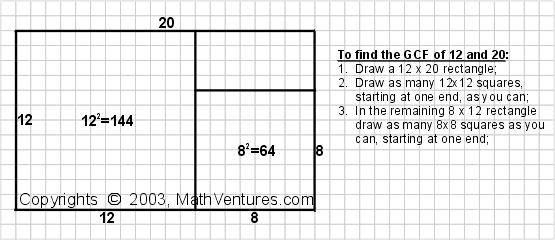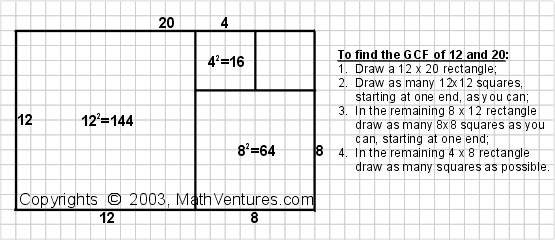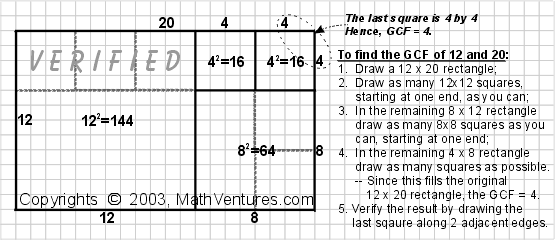
Say the two numbers for which you want to find the GCF are m and n. Let us say that m > n. (the case for m < n is symetric and we can reverse the roles of the numbers either in the inequality or in the procedure. If m = n then there is nothing to do because the LCF = m = n.)
 

1. Draw an m by n rectangle;
2. Draw the largest possible square inside this rectangle -- that is, draw a nxn square -- such that one of its corners coincides with one of the corners of the rectangle. We call the leftover rectangle the remaining rectangle. In this case the dimensions of the remaining rectangle are nx(m-n), where n >= (m-n).
3. If the remaining rectangle is a square -- that is n = (m-n) -- stop. Your GCF equals the length of one edge of this square, which I call the GCF square.
4. Otherwise, repeat Step 2 and Step 3 in each remaining rectangle. In other words, as long as n > (m-n), substitute n for m and (m-n) for n and repeat Step 2.
5. To confirm the result, replicate the GCF square along each edge of the large rectangle, starting at one corner. The GCF square should fit along each side an integer number of times. Putting it in mathematical terms, if the GCF square fits along the m edge p times and along the n edge q times, then both p and q must be integers. If even one of them is not, then there is a mistake in the drawing and either the result or the confirmation is incorrect.

To Observe and Figure-out Why
 
• Notice that p and q are not equal.
• Also, most likely neither p nor q is equal to 1. If either equals 1 then the longer edge is a multiple of the short edge.

Why This Works?

Explanation 1. By replicating The GCF square along the edges of the original rectangle during the confirmation phase (Step 5) you perform division — you divide the length of the edge by the size of the GCF square. This step clearly shows that the GCF square is indeed a common factor (divisor). It is the largest common factor (divisor) because during the procedure you tested every possible number that is a factor (divisor) of one of the rectangle edges by representing these numbers with squares of diminishing sizes.

Explanation 2. When you repeatedly draw the same largest possible square in a rectangle (this happens once in Example 1 with the 4x4 squares and twice in Example 2 with the 7x7 and with the 1x1 squares), you perform division by doing repeated subtraction. That is, this method substitutes repeated subtraction for division. As such, it is simpler then having to divide. Furthermore, since no division is required, you also do not have to figure out any divisor (factor) of either number. It is a simplified version of the procedure known as Euclidean algorithm.
 

Finding the LCF (LCD) of Large Numbers?

Large numbers pose a practical limitation for this method. Drawing to scale, factoring large numbers with this method requires a correspondingly large drawing surface (e.g., sheet of paper, whiteboard) and/or very precise minute-drawing skill (using such tools as graph paper, snap cubes, whiteboard and a ruler). If either such tools or skills are not available, then one is limited with resepct to the size of the numbers he or she can factor.

There is a way around this limitation.

Once you understand and are comfortable with this graphic method, you can draw not to scale and use it to figure out the GCF of any two integers. The trade off is that when you factor large number using not-to-scale drawing, you must perform subtractions, each time you draw a "not to scale square", you subtract its size from the the size of the rectangle's edge along which you draw it. In a sense, what you have to do is explicitly compute the subtraction that, when drawing to scale, the act of drawing performs for you implicitly.

Although you must compute, subraction is simpler than division. Moreover subraction is straight-forward comparing with figuring out the divisors (factors) of large numbers, which for most people is a time-consuming and tedious trail-and-error process.
 
 

Download Finding the Greatest Common Factor Graphically

Download Instructions

  *   More direct links cannot be given here because these sites are changed frequently. These links open in a separate window so you do not lose your place here.